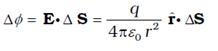Loss of Energy on Sharing Charges

Loss of Energy on Sharing of Charges between the Capacitors in Parallel: Consider two capacitors of capacitances C1, C2, charges q1, q2 and potentials V1,V2.

Total charge after sharing = Total charge before sharing

V is known as common potential.

Therefore, there is some loss of energy when two charged capacitors are connected together. The loss of energy appears as heat and the wire connecting the two capacitors may become hot.

Energy Density of a Parallel Plate Capacitor

Energy Density

SI unit of energy density is J m-3.
Energy density is generalized as energy per unit volume of the field.

Total Energy Stored in a Combination of Capacitor

Series Combination of Capacitors
Energy Stored in a Series Combination of Capacitors:

The total energy stored in the system is the sum of energy stored in the individual capacitors.


Parallel Combination of Capacitors

The total energy stored in the system is the sum of energy stored in the individual capacitors.

Energy Stored in a Capacitor

To determine the energy stored in capacitor, consider initially two uncharged conductors 1 and 2. Imagine next a process of transferring charge from conductor 2 to conductor 1 bit by bit, so that at the end, conductor 1 gets charge Q.

By charge conservation, conductor 2 has charge –Q at the end.

In transferring positive charge from conductor 2 to conductor 1, work will be done externally, since at any stage conductor 1 is at a higher potential than conductor 2.

To calculate the total work done, we first calculate the work done in a small step involving transfer of an infinitesimal (i.e., vanishingly small) amount of charge. Consider the intermediate situation when the conductors 1 and 2 have charges Q' and –Q' respectively. At this stage, the potential difference V^' between conductors 1 to 2 are Q' /C, where C is the capacitance of the system.

Next imagine that a small charge δQ'  is transferred from conductor 2 to 1. Work done in this step (δW' ), resulting in charge Q' on conductor 1 increasing to Q' + δQ' , is given by

The total work done (W) is the sum of the small work (δ W) over the very large number of steps involved in building the charge Q^' from zero to Q.

The same result can be obtained directly from Eq. by integration

The surface charge density s is related to the electric field E between the plates,

Grouping of Capacitors

Capacitors in series

Figure shows capacitors C₁ and C₂ combined in series.

The left plate of C₁ and the right plate of C₂ are connected to two terminals of a battery and have charges Q and –Q, respectively.

It then follows that the right plate of C₁ has charge –Q and the left plate of C2 has charge Q. If this was not so, the net charge on each capacitor would not be zero.

This would result in an electric field in the conductor connecting C₁and C₂. Charge would flow until the net charge on both C₁ and C₂ is zero and there is no electric field in the conductor connecting C₁ and C₂. Thus, in the series combination, charges on the two plates (±Q) are the same on each capacitor.

The total potential drop V across the combination is the sum of the potential drops V and V across C and C, respectively.

Following the same steps as for the case of two capacitors, we get the general formula for effective capacitance of a series combination of n capacitors:

Capacitors in parallel

Figure shows two capacitors arranged in parallel. In this case, the same potential difference is applied across both the capacitors.

But the plate charges (±Q₁) on capacitor 1 and the plate charges (±Q₂) on the capacitor 2 are not necessarily the same:

Relative Permittivity or Dielectric Constant

We have two large plates, each of area A, separated by a distance d. The charge on the plates is ±Q, corresponding to the charge density ±σ (with σ = Q/A). When there is vacuum between the plates,

Consider next a dielectric inserted between the plates fully occupying the intervening region. The dielectric is polarised by the field, the effect is equivalent to two charged sheets (at the surfaces of the dielectric normal to the field) with surface charge densities σ p and –σ p.

The electric field in the dielectric then corresponds to the case when the net surface charge density on the plates is ±(σ– σ p ). That is,

So that the potential difference across the plates is

For linear dielectrics, we expect σ p to be proportional to ε₀, i.e., to σ. Thus, (σ– σ p ) is proportional to σ and we can write

Parallel Plate Capacitor

A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance.

Let A be the area of each plate and d the separation between them. The two plates have charges Q and –Q.

Since d is much smaller than the linear dimension of the plates (d² << A), we can use the result on electric field by an infinite plane sheet of uniform surface charge density.

Plate 1 has surface charge density σ = Q/A and plate 2 has a surface charge density –σ. The electric field in different regions is:

Outer region I (region above the plate 1),

The direction of electric field is from the positive to the negative plate.

Thus, the electric field is localised between the two plates and is uniform throughout. For plates with finite area, this will not be true near the outer boundaries of the plates. The field lines bend outward at the edges – an effect called ‘fringing of the field’.

Now for uniform electric field, potential difference is simply the electric field times the distance between the plates, that is,

Principle of Capacitance

Step 1: Plate A is positively charged and B is neutral. 

Step 2: When a neutral plate B is brought near A, charges are induced on B such that the side near A is

negative and the other side is positive. The potential of the system of A and B in step 1 and 2 remains the same because the potential due to positive and negative charges on B cancel out.

Step 3: When the farther side of B is earthed the positive charges on B get neutralised and B is left only

with negative charges. 

Now, the net potential of the system decreases due to the sum of positive potential on A and negative potential on B. 

To increase the potential to the same value as was in step 2, an additional amount of charges can be given to plate A. 

This means, the capacity of storing charges on A increases.The system so formed is called a ‘capacitor’.

Capacity of an Isolated Spherical Conductor

Let a charge q be given to the sphere which is assumed to be concentrated at the centre. Potential at any point on the surface is

1. Capacitance of a spherical conductor is directly proportional to its radius.
2. The above equation is true for conducting spheres, hollow or solid.
3. If the sphere is in a medium, then C = 4πε0εr.R
4. Capacitance of the earth is 711 μF.

Electrical Capacitance

CAPACITORS AND CAPACITANCE

A capacitor is a system of two conductors separated by an insulator. The conductors have charges; say Q₁ and Q₂, and potentials V₁ and V₂.

Usually, in practice, the two conductors have charges Q and – Q, with potential difference V = V₁ – V₂ between them.

The conductors may be so charged by connecting them to the two terminals of a battery. Q is called the charge of the capacitor, though this, in fact, is the charge on one of the conductors – the total charge of the capacitor is zero.

The electric field in the region between the conductors is proportional to the charge Q. That is, if the charge on the capacitor is, say doubled, the electric field will also be doubled at every point.

Potential difference V is the work done per unit positive charge in taking a small test charge from the conductor 2 to 1 against the field.

 Consequently, V is also proportional to Q, and the ratio Q/V is a constant C.

The constant C is called the capacitance of the capacitor. C is independent of Q or V, as stated above.

The capacitance C depends only on the geometrical configuration (shape, size, separation) of the system of two conductors.

The SI unit of capacitance is 1 farad (=1 coulomb volt^-1) or 1 F = 1 C V^–1. A capacitor with fixed capacitance is symbolically shown as ---||---.

A capacitor with large capacitance can hold large amount of charge Q at a relatively small V.

High potential difference implies strong electric field around the conductors.

The maximum electric field that a dielectric medium can withstand without break-down (of its insulating property) is called its dielectric strength; for air it is about 3 × 10e6 Vm^–1. 

Electrostatic Shielding

Whatever be the charge and field configuration outside, any cavity in a conductor remains shielded from outside electric influence: the field inside the cavity is always zero. This is known as electrostatic shielding.

The effect can be made use of in protecting sensitive instruments from outside electrical influence.

Electrostatics of Conductors

Conductors contain mobile charge carriers. In metallic conductors, these charge carriers are electrons. In a metal, the outer (valence) electrons part away from their atoms and are free to move. These electrons are free within the metal but not free to leave the metal.

In an external electric field, they drift against the direction of the field. The positive ions made up of the nuclei and the bound electrons remain held in their fixed positions. In electrolytic conductors, the charge carriers are both positive and negative ions.

Important results regarding electrostatics of conductors.

1.   Inside a conductor, electrostatic field is zero

In the static situation, the free charges have so distributed themselves that the electric field is zero everywhere inside. Electrostatic field is zero inside a conductor.

2. At the surface of a charged conductor, electrostatic field must be normal to the surface at every point

In the static situation, therefore, E should have no tangential component. Thus electrostatic field at the surface of a charged conductor must be normal to the surface at every point.

3. The interior of a conductor can have no excess charge in the static situation.

There is no net charge at any point inside the conductor, and any excess charge must reside at the surface.

4. Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface

Since E = 0 inside the conductor and has no tangential component on the surface, no work is done in moving a small test charge within the conductor and on its surface. That is, there is no potential difference between any two points inside or on the surface of the conductor.

5. Electric field at the surface of a charged conductor

where σ is the surface charge density and nˆ is a unit vector normal to the surface in the outward direction.

Electric Field Intensity due to two Sheet of Charge

Electric Field Intensity due to Spherical Shell

Field due to a uniformly charged thin spherical shell

Let σ be the uniform surface charge density of a thin spherical shell of radius R. The field at any point P, outside or inside, can depend only on r (the radial distance from the centre of the shell to the point) and must be radial (i.e., along the radius vector).

(i)         Field outside the shell: Consider a point P outside the shell with radius vector r. To calculate E at P, we take the Gaussian surface to be a sphere of radius r and with centre O, passing through P. All points on this sphere are equivalent relative to the given charged configuration. The electric field at each point of the Gaussian surface, therefore, has the same magnitude E and is along the radius vector at each point.

Thus, E and ΔS at every point are parallel and the flux through each element is E ΔS. Summing over all ΔS, the flux through the Gaussian surface is E × 4 π r². The charge enclosed is σ × 4 π R². By Gauss’s law

The electric field is directed outward if q > 0 and inward if q < 0. This, however, is exactly the field produced by a charge q placed at the centre O. Thus for points outside the shell, the field due to a uniformly charged shell is as if the entire charge of the shell is concentrated at its centre.

(ii) Field inside the shell: In Fig., point P is inside the shell. The Gaussian surface is again a sphere through P centred at O.

The flux through the Gaussian surface, calculated as before, is E × 4 π r². However, in this case, the Gaussian surface encloses no charge. Gauss’s law then gives E × 4 π r² = 0 i.e., E = 0 (r < R).

The field due to a uniformly charged thin shell is zero at all points inside the shell. This important result is a direct consequence of Gauss’s law which follows from Coulomb’s law. 

Electric Field Intensity due to Sheet of Charge

Field due to a uniformly charged infinite plane sheet

Let σ be the uniform surface charge density of an infinite plane sheet. We take the x-axis normal to the given plane. By symmetry, the electric field will not depend on y and z coordinates and its direction

We can take the Gaussian surface to be a rectangular parallelepiped of cross sectional area A, as shown. (A cylindrical surface will also do.) As seen from the figure, only the two faces 1 and 2 will contribute to the flux; electric field lines are parallel to the other faces and they, therefore, do not contribute to the total flux.

The unit vector normal to surface 1 is in –x direction while the unit vector normal to surface 2 is in the +x direction. Therefore, flux E.ΔS through both the surfaces are equal and add up. Therefore the net flux through the Gaussian surface is 2 EA. The charge enclosed by the closed surface is σ A. Therefore by Gauss’s law,

 where nˆ is a unit vector normal to the plane and going away from it. E is directed away from the plate if σ is positive and toward the plate if σ is negative.

Note that the above application of the Gauss’ law has brought out an additional fact: E is independent of x also

Deduction of Coulomb’s Law from Gauss’s Theorem

Applications of Gauss’s Theorem

Field due to an infinitely long straight uniformly charged wire

Consider an infinitely long thin straight wire with uniform linear charge density λ. The direction of electric field at every point must be radial (outward if λ > 0, inward if λ < 0).

Consider a pair of line elements P₁ and P₂ of the wire, as shown. The electric fields produced by the two elements of the pair when summed give a resultant electric field which is radial (the components normal to the radial vector cancel).

To calculate the field, imagine a cylindrical Gaussian surface, as shown in the Fig. Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero.

At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, s ince it depends only on r.

The surface area of the curved part is 2Πrl, where l is the length of the cylinder.

where nˆ is the radial unit vector in the plane normal to the wire passing through the point. E is directed outward if λ is positive and inward if λ is negative. 

Gauss’s Theorem and its Proof

GAUSS’S LAW

The surface integral of electrostatic field E produce by any source over any closed surface S enclosing a volume V in vacuum i.e. total electric flux over the closed surface S in vacuum is 1/epsilon times the total charge Q contained inside S.

                                          

The surface chosen to calculate the surface integral is called Gaussian surface.

PROOF OF GAUSSIAN THEOREM

The flux through area element ΔS is

The unit vector rˆ is along the radius vector from the centre to the area element. Now, since the normal to a sphere at every point is along the radius vector at that point, the area element ΔS and rˆ have the same direction. Therefore,

 Since the magnitude of a unit vector is 1. The total flux through the sphere is obtained by adding up flux through all the different area elements:

 Since each area element of the sphere is at the same distance r from the charge,

SIGNIFICANCE OF GAUSS’S LAW

(i)                 Gauss’s law is true for any closed surface, no matter what its shape or size.

(ii)               The term q on the right side of Gauss’s law includes the sum of all charges enclosed by the surface. The charges may be located anywhere inside the surface.

(iii)             In the situation when the surface is so chosen that there are some charges inside and some outside, the electric field is due to all the charges, both inside and outside S. The term q on the right side of Gauss’s law.

(iv)              Gauss’s law is often useful towards a much easier calculation of the electrostatic field when the system has some symmetry. This is facilitated by the choice of a suitable Gaussian surface.

(v)                Finally, Gauss’s law is based on the inverse square dependence on distance contained in the Coulomb’s law. Any violation of Gauss’s law will indicate departure from the inverse square law. 

Electric Flux

 Electric flux over an area in an electric field represents the total number of field lines crossing this area.

The number of field lines crossing a unit area, placed normal to the field at a point is a measure of the strength of electric field at that point.

If we place a small planar element of area ΔS normal to E at a point, the number of field lines crossing it is proportional to E ΔS.

If we tilt the area element by angle θ, the number of field lines crossing the area element will be smaller. The projection of the area element normal to E is ΔS cosθ.

Thus, the number of field lines crossing ΔS is proportional to E ΔS cosθ. Hence

Area Vector

Area is a scalar quantity, but in some the problems, it is convenient to treat it as vector. A small area can be treated as planar. As normal to the plane specifies the orientation of plane, therefore, the direction of planar area vector is along its normal.

By convention, the vector associated with every area element of a closed surface is taken to be in the direction of the outward normal.

Potential Energy of A System of Charges

Consider the charges q₁ and q₂ initially at infinity and determine the work done by an external agency to bring the charges to the given locations.

Suppose, charge q₁ is brought from infinity to the point r₁. There is no external field against which work needs to be done, so work done in bringing q₁ from infinity to r₁ is zero. This charge produces a potential in space given by

where r_1P is the distance of a point P in space from the location of q₁.

From the definition of potential, work done in bringing charge q₂ from infinity to the point r₂ is q times the potential at r₂ due to q₁:

where r₁₂ is the distance between points 1 and 2.

If q₁q₂ > 0, Potential energy is positive. For unlike charges (q₁ q₂ < 0), the electrostatic force is attractive.

Potential energy of a system of three charges q₁, qand q located at r₁, r₂, r, respectively. To bring q first from infinity to r₁, no work is required. Next bring q₂ from infinity to r₂. As before, work done in this step is

The total work done in assembling the charges at the given locations is obtained by adding the work done in different steps,

 The potential energy is characteristic of the present state of configuration, and not the way the state is achieved.