Electric Flux

 Electric flux over an area in an electric field represents the total number of field lines crossing this area.

The number of field lines crossing a unit area, placed normal to the field at a point is a measure of the strength of electric field at that point.

If we place a small planar element of area ΔS normal to E at a point, the number of field lines crossing it is proportional to E ΔS.

If we tilt the area element by angle θ, the number of field lines crossing the area element will be smaller. The projection of the area element normal to E is ΔS cosθ.

Thus, the number of field lines crossing ΔS is proportional to E ΔS cosθ. Hence

Area Vector

Area is a scalar quantity, but in some the problems, it is convenient to treat it as vector. A small area can be treated as planar. As normal to the plane specifies the orientation of plane, therefore, the direction of planar area vector is along its normal.

By convention, the vector associated with every area element of a closed surface is taken to be in the direction of the outward normal.

Potential Energy of A System of Charges

Consider the charges q₁ and q₂ initially at infinity and determine the work done by an external agency to bring the charges to the given locations.

Suppose, charge q₁ is brought from infinity to the point r₁. There is no external field against which work needs to be done, so work done in bringing q₁ from infinity to r₁ is zero. This charge produces a potential in space given by

where r_1P is the distance of a point P in space from the location of q₁.

From the definition of potential, work done in bringing charge q₂ from infinity to the point r₂ is q times the potential at r₂ due to q₁:

where r₁₂ is the distance between points 1 and 2.

If q₁q₂ > 0, Potential energy is positive. For unlike charges (q₁ q₂ < 0), the electrostatic force is attractive.

Potential energy of a system of three charges q₁, qand q located at r₁, r₂, r, respectively. To bring q first from infinity to r₁, no work is required. Next bring q₂ from infinity to r₂. As before, work done in this step is

The total work done in assembling the charges at the given locations is obtained by adding the work done in different steps,

 The potential energy is characteristic of the present state of configuration, and not the way the state is achieved.

Potential Energy In An External Field

Potential energy of a single charge

The external electric field E and the corresponding external potential V may vary from point to point. By definition, V at a point P is the work done in bringing a unit positive charge from infinity to the point P.

Work done in bringing a charge q from infinity to the point P in the external field is qV. This work is stored in the form of potential energy of q. If the point P has position vector r relative to some origin, we can write:

 Potential energy of a system of two charges in an external field

Work done in bringing the charge q₁ from infinity to r₁ is q₁ V(r₁). Consider the work done in bringing q₂ to r₂. In this step, work is done not only against the external field E but also against the field due to q₁.

Work done on q₂ against the external field

Work done on q₂ against the field due to q₁

  

By superposition principle for fields, add up the work done on q₂ against the two fields. Work done in bringing q₂ to r₂

 Thus, Potential energy of the system = the total work done in assembling the configuration

Relation Between Field And Potential

Consider two closely spaced equipotential surfaces A and B Fig. with potential values V and V + δV, where δV is the change in V in the direction of the electric field E.

Let P be a point on the surface B. δl is the perpendicular distance of the surface A from P. Imagine that a unit positive charge is moved along this perpendicular from the surface B to surface A against the electric field. The work done in this process is |E|δl.

This work equals the potential difference V_A –V_B. Thus,

We thus arrive at two important conclusions concerning the relation between electric field and potential:

(i)            Electric field is in the direction in which the potential decreases steepest

(ii)           Its magnitude is given by the change in the magnitude of potential per unit displacement normal to the equipotential surface at the point.

Equipotential Surfaces

An equipotential surface is a surface with a constant value of potential at all points on the surface. For a single charge q, the potential is given by

This shows that V is a constant if r is constant. Thus, equipotential surfaces of a single point charge are concentric spherical surfaces centre at the charge.

No work in done in moving from one point to another in equipotential surface.

For a uniform electric field E, say, along the x -axis, the equipotential surfaces are planes normal to the x -axis, i.e., planes parallel to the y-z plane. Equipotential surfaces for (a) a dipole and (b) two identical positive charges are shown in Fig.

Potential Due To An Electric Dipole

Take the origin at the centre of the dipole. Since potential is related to the work done by the field, electrostatic potential also follows the superposition principle. Thus, the potential due to the dipole is the sum of potentials due to the charges q and –q

where r₁ and r₂ are the distances of the point P from q and –q, respectively.

Now, by geometry,

Take r much greater than a ( r >> a ) and retain terms only up to the first order in a/r

 Using the Binomial theorem and retaining terms up to the first order in a/r; obtain,

where rˆ is the unit vector along the position vector OP. The electric potential of a dipole is then given by

Equation is approximately true only for distances large compared to the size of the dipole, so that higher order terms in a/r are negligible. For a point dipole p at the origin,

From Eq. potential on the dipole axis (θ= 0, π) is given by

(Positive sign for θ= 0, negative sign for θ= π.) The potential in the equatorial plane (θ= π/2) is zero.

(i)                 The potential due to a dipole depends not just on r but also on the angle between the position vector r and the dipole moment vector p.

(ii)               The electric dipole potential falls off, at large distance, as 1/r₂, not as 1/r, characteristic of the potential due to a single charge.

Potential Due To A System Of Charges

Consider a system of charges q₁, q₂,…, qn with position vectors r₁, r₂,…, r _n relative to some origin. The potential V₁ at P due to the charge q₁ is

 where r_1P is the distance between q₁  and _P. Similarly, the potential V₂ at P due to q₂ and due to q are given by

where r_2P and r_3P are the distances of P from charges q₂ and q₃, respectively; and so on for the potential due to other charges.

By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charges

The electric field outside the shell is as if the entire charge is concentrated at the centre. Thus, the potential outside the shell is given by

where q is the total charge on the shell and R its radius. The electric field inside the shell is zero. This implies that potential is constant inside the shell (as no work is done in moving a charge inside the shell), and, therefore, equals its value at the surface, which is

Potential Due To A Point Charge

Consider a point charge Q at the origin. For Q > 0, the work done against the repulsive force on the test charge is positive. Choose a convenient path along the radial direction from infinity to the point P.

At some intermediate point P′ on the path, the electrostatic force on a unit positive charge is

where rˆ′ is the unit vector along OP′. Work done against this force from r′ to r′ + ∆r′ is

The negative sign appears because for ∆r′ < 0, ∆W is positive. Total work done (W) by the external force is obtained by integrating from r′ = ∞ to r′ = r,

This, by definition is the potential at P due to the charge Q

 Figure below shows how the electrostatic potential ( ∝ 1/r) and the electrostatic field ( ∝ 1/r² ) varies with r.

Electrostatic Potential

Work done per unit test charge is characteristic of the electric field associated with the charge configuration. This leads to the idea of electrostatic potential V due to a given charge configuration.

Work done by external force in bringing a unit positive charge from point R to P

where V_P and V_R are the electrostatic potentials at P and R, respectively.

Work done by an external force in bringing a unit positive charge from infinity to a point = electrostatic potential (V) at that point.

 In other words, the electrostatic potential (V) at any point in a region with electrostatic field is the work done in bringing a unit positive charge (without acceleration) from infinity to that point.

SI unit of Potential difference is Volt. 1V=1Nm C^-1

___________________________________________________________________________________________

Some of these questions which may be asked in your Board Examination 2012-2013

Q1: When a plastic comb is passed through dry hair, what type of charge is acquire by comb?

Q2: Does motion of a body affect its charge?

Q3: What is the origin of frictional forces?

Answer these questions in comment box and help your friends

Electric Potential Energy

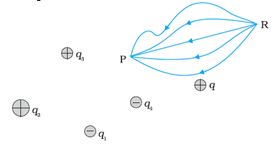
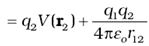Consider an electrostatic field E due to a charge Q placed at the origin. Now, bring a test charge q from a point R to a point P against the repulsive force on it due to the charge Q. This will happen if Q and q are either positive or both negative.

 

 Take Q, q > 0. First, assume that the test charge q is so small that it does not disturb the original configuration.

Second, in bringing the charge q from R to P, apply an external force F_ext just enough to counter the repulsive electric force FE (i.e, F_ext= –F_E).

This means there is no net force on or acceleration of the charge q when it is brought from R to P, i.e., it is brought with infinitesimally slow constant speed.

Work done by the external force is the negative of the work done by the electric force, and gets fully stored in the form of potential energy of the charge q.

If the external force is removed on reaching P, the electric force will take the charge away from Q – the stored energy (potential energy) at P is used to provide kinetic energy to the charge q in such a way that the sum of the kinetic and potential energies is conserved.

Thus, work done by external forces in moving a charge q from R to P is

At every point in electric field, a particle with charge q possesses a certain electrostatic potential energy, this work done increases its potential energy by an amount equal to potential energy difference between points R and P.

Thus, potential energy difference

 (Note here that this displacement is in an opposite sense to the electric force and hence work done by electric field is negative, i.e., –W_RP.) 

Therefore, can define electric potential energy difference between two points as the work required to be done by an external force in moving (without accelerating) charge q from one point to another for electric field of any arbitrary charge configuration.

  

Two important comments may be made at this stage:

(i) Work done by an electrostatic field in moving a charge from one point to another depends only on the initial and the final points and is independent of the path taken to go from one point to the other. This is the fundamental characteristic of a conservative force.

  

(ii) A convenient choice is to have electrostatic potential energy zero at infinity. With this choice, if take the point R at infinity,

 Potential energy of charge q at a point (in the presence of field due to any charge configuration) is the work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that point.

___________________________________________________________________________________________

Some of these questions which may be asked in your Board Examination 2012-2013

Q1: When a plastic comb is passed through dry hair, what type of charge is acquire by comb?

Q2: Does motion of a body affect its charge?

Q3: What is the origin of frictional forces?

Answer these questions in comment box and help your friends

An Organized Student

"A successful student, is an organized student!"

The main aspects of staying focused and organized with school work are:

•  always paying attention 
•  always making direct eye contact with the teacher 
•  always coming to class with all school materials (pen, pencil, eraser, etc.) 
•  always coming to class with all homework done 
•  making neat and complete notes in the planner 
•  asking the teacher questions if having trouble or if not able to understand  something 
•  never cheating or copying homework or any other assignments 
•  reviewing lessons daily, for class tests and quizzes 
•  always studying for class tests and quizzes in advance 
•  when studying or completing homework find a quiet, well lit place so as not to be distracted 
• avoiding talking or disturbing other pupils in class, the more focused they  stay on homework, the faster it will get done, and it will be quality work 
• always challenging the self to stay on task and meeting all deadlines by finishing all homework 
• prioritizing homework by starting with the easiest work first and the harder  work last or visa-versa 
• rewarding the self once one of the goals is met i.e. by taking a break or treating the self 
• creating a homework kit for emergencies when needing to do homework and  have forgotten materials at school (pencil, pen, paper, eraser, calculator, dictionary, etc.) 
• color coding all files etc. for organization and easy studying 
• keeping a daily record guide or planner for own personal reasons with plans to co-ordinate homework, chores, extra-curricular activities and other special events 

In conclusion, to be a successful student in school simply follow the helpful steps above and your education will not only be fun but it will be rewarding.

A Good Study Place

A Good Study Place

Following are the guidelines to make a place in your home a good study place.

1. Study place should be accessible anytime you want

It is good if you have a room in your house which is specially dedicated to you as you can access it whenever you like. If you are sharing common place for study with your family member, then try to develop a common understand when both of you  or you alone can use it anytime.

2. Study Place should be free from any kind of disturbance

Choose a place in your hose which is less visited by other family members. This is reduce unnecessary disturbance created by others. You can always put a DO NOT DISTURB board on the door or on front wall of the study table which is visible to all. If you are using mobile phone or internet try to switched off these before you start studying..

3. Study Place should be free from noise as far as possible

For study, your place should free from noise it may be because of talking of your family or TV running in next room. Always make sure that all the family member are aware that you are studying and  need no distraction. You can always ask for volume to be low.

4. Study Place  should have all study material available

Make sure that all the books and notes are available with you when you start studying. Study material may contain  pens and pencils, paper, ruler etc.

5. Study Space should have comfortable table and chair?

Study room should have a table which can accommodate all your belongings and still have sufficient area for the study. You need a good chair having good adjustment feature. If you are uncomfortable with chair it will distract you from the study.

6. Study Place have sufficient light or a good table lamp

Just to avoid eye stress, arrange for the sufficient amount of light in your study room. You may always has the table lamp. Table lamp help you to keep concentrated on you table only as everything else will be in dark.

7. Study Place should have a maintained temperature

Concentration in study depend on your body temperature. Hence is necessary the surrounding temperature is maintained to keep your body temperature under control. Use AC or fan in summary and room heater in winter.

Physics Paper - 2012 (Set 3) - CBSE