The capacitance for spherical or cylindrical conductors can be obtained by evaluating the voltage difference between the conductors for a given charge on each. By applying Gauss' law to an charged conducting sphere, the electric field outside it is found to be
The voltage between the spheres can be found by integrating the electric field along a radial line:

From the definition of capacitance, the capacitance is
For a cylindrical geometry like a coaxial cable, the capacitance is usually stated as a capacitance per unit length. The charge resides on the outer surface of the inner conductor and the inner wall of the outer conductor. The capacitance expression is




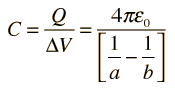

No comments:
Post a Comment