Potential energy of a single charge
The external electric field E and the corresponding external
potential V may vary from point to point. By definition, V at a point P is the
work done in bringing a unit positive charge from infinity to the point P.
Work done in bringing a charge q from infinity to the point P in
the external field is qV. This work is stored in the form of potential energy
of q. If the point P has position vector r relative to some origin, we can
write:
Work done in bringing the charge q1 from infinity to
r1 is q1 V(r1). Consider the work done in
bringing q2 to r2. In this step, work is done not only
against the external field E but also against the field due to q1.
Work done on q2 against the external field
Work done on q2 against the field due to q1
By superposition principle for fields, add up the work done on q2
against the two fields. Work done in bringing q2 to r2




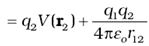

The work done is against the electric field then why there is no negative sign
ReplyDeleteElectric field is a vector quantity
DeleteI have a mission that I’m just now working on, and I have been at the look out for such information external electric window shutters
ReplyDeleteReally nice and interesting post. I was looking for this kind of information and enjoyed reading this one. check my reference
ReplyDeleteWe are tied directly into the sate’s renewal database which allows us to process your request almost instantly. see post
ReplyDelete